The Critical Role of Aerodynamics: Insights from the NASA-BeVERLI Hill Experiment

Introduction

Virginia Tech Stability Wind Tunnel Fan — Figure 1: The fan of the Virginia Tech Stability Wind Tunnel

Aerodynamics plays a central role in aerospace engineering, shaping everything from aircraft design to space vehicle performance and safety. In this post, I share what I learned from a wind tunnel experiment I conducted as part of my Experimental Methods course in Fall 2023 at Virginia Tech. Among several experiments, the Stability Wind Tunnel study—part of the BeVERLI Hill Project, a NASA-sponsored initiative—stood out to me. It gave me valuable experience with both practical testing and data analysis, and helped me better understand the challenges of studying complex aerodynamic flows.

Summary of Experiment

Since drag is an essential factor in aerodynamic performance, analyzing pressure distribution and the boundary layer is key to predicting how a body behaves in flow. One of the big challenges in the aerospace industry is studying unsteady, turbulent flow and boundary layer separation over three-dimensional curved surfaces. To address this, the BeVERLI (Benchmark Validation Experiments for RANS/LES Investigations) Hill project was created to generate high-fidelity experimental data that can validate turbulence models used in Computational Fluid Dynamics (CFD).

RANS (Reynolds-Averaged Navier-Stokes) is a method that averages the Navier-Stokes equations over time to predict mean flow behavior, modeling the effects of turbulence through turbulence models. The Navier-Stokes equations describe the motion of viscous fluid substances.

\rho (\frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u}) = -\nabla p + \mu \nabla^2 \mathbf{u} + \rho \mathbf{g}

where:

$\rho$ : fluid density
$\mathbf{u}$ : fluid velocity vector field
$t$ : time
$p$ : pressure
$\mu$ : dynamic viscosity
$\mathbf{g}$ : gravitational acceleration
$\nabla$ : gradient operator

In contrast, LES (Large Eddy Simulation) directly resolves the larger turbulent structures while modeling only the smaller scales, offering more detailed predictions. The filtered governing equations for LES describe the large-scale structures, while the small-scale effects are represented through subgrid models.

\frac{\partial \overline{u_i}}{\partial t} + \overline{u_j} \frac{\partial \overline{u_i}}{\partial x_j} = -\frac{1}{\rho} \frac{\partial \overline{p}}{\partial x_i} + \nu \frac{\partial^2 \overline{u_i}}{\partial x_j \partial x_j} - \frac{\partial \tau_{ij}}{\partial x_j}

where:

$\overline{u_i}$ : filtered velocity component in the i-th direction
$\overline{p}$ : filtered pressure
$\nu$ : kinematic viscosity
$\tau_{ij}$ : subgrid-scale stress tensor

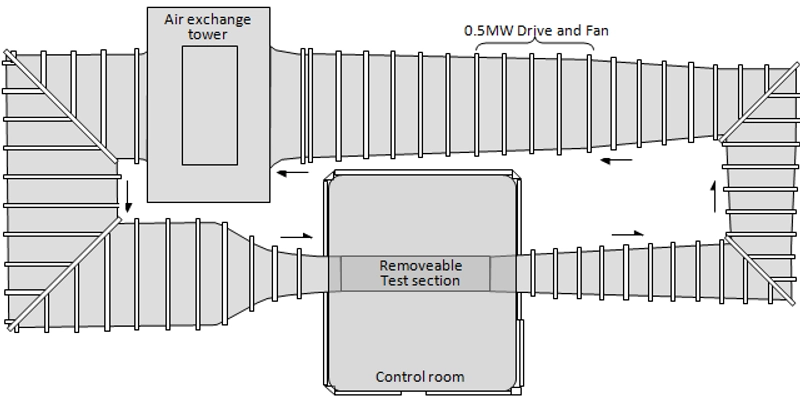
Schematic view of Virginia Tech Stability Wind Tunnel — Figure 2: Schematic diagram showing the layout of the Virginia Tech Stability Wind Tunnel

The Virginia Tech Stability Wind Tunnel is one of the largest university-operated wind tunnels in the U.S., with a 1.85m × 1.85m test section. Its closed-circuit design continuously recirculates air, offering advantages such as better flow quality, reduced power requirements, and improved temperature control. With speeds up to 80 m/s (Reynolds number ~5,000,000 per meter), it is well suited for precise aerodynamic testing and uncertainty analysis—making it an ideal facility for the BeVERLI Hill project.

The experiment I worked on was the sixth in the series, focusing on wall pressure signatures over a smooth bump at Reynolds numbers of 250,000 and 650,000. These values were chosen to capture the transition from laminar to turbulent flow under subsonic conditions.

My objectives for the experiment were:

To measure the mean wall pressure distribution around the BeVERLI hill at the two Reynolds numbers and compare the uncertainties in the pressure coefficient.
To evaluate unsteady wall pressure using power spectral density (PSD) at each Reynolds number, including mean and variance calculations from four pressure taps.

Because turbulent boundary layers are inherently unsteady, I used PSD analysis to separate the fluctuating signals into frequency components. This provided insight into how energy is distributed across frequencies—a key aspect of analyzing unsteady forces. To strengthen the validity of my results, I also performed a detailed uncertainty analysis.

Wind Tunnel Test Section — Figure 3: The test section of the wind tunnel, with the BeVERLI hill model mounted on the left wall. The model’s placement allows for precise measurement of wall pressure distributions and flow characteristics.

Key concepts for the experiment

Understanding laminar and turbulent flow is crucial in aerodynamics. With its chaotic eddies and vortices, turbulent flow significantly impacts drag, lift, and overall performance, making analysis more complex than laminar flow’s smooth, predictable nature. The Reynolds number is key in predicting the transition from laminar to turbulent flow, directly influencing drag forces.

Pressure coefficient

The compressible version of the pressure coefficient $C_p$ is given by the following equation:

C_p = \frac{p - p_\infty}{\frac{1}{2} \gamma p_\infty M_\infty^2}

Where:

$p$ : local static pressure
$p_{\infty}$ : free-stream static pressure
$\gamma$ : specific heat ratio (typically 1.4 for air)
$M_{\infty}$ : free-stream Mach number

Boundary Layer

The boundary layer is a thin region near an object’s surface where viscous forces dominate. It is crucial for determining drag, lift, and flow separation. Flow separation occurs when this layer detaches, increasing drag and causing potential instability.

Reynolds Number

The Reynolds number is a dimensionless quantity representing the ratio of inertial to viscous forces in a fluid flow:

Re=\frac{\rho U L}{\mu}

where:

$\rho$ : fluid density
$U$ : flow velocity
$L$ : characteristic length (e.g., chord length of an airfoil)
$\mu$ : dynamic viscosity

Mach Number

The Mach number represents the ratio of flow velocity to the speed of sound in the fluid:

M=\frac{U}{a}=\frac{U}{\sqrt{\gamma R T}}

where:

$U$ : flow velocity
$a$ : speed of sound in the fluid
$\gamma$ : specific heat ratio
$R$ : gas constant
$T$ : absolute temperature

Spectral analysis

Spectral analysis uses the Fourier Transform to convert a time-domain signal into its frequency components:

\mathcal{F}(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} \, dt

where:

$\mathcal{F}(\omega)$ : Fourier transform of the signal
$f(t)$ : original time-domain signal
$\omega$ : angular frequency
$t$ : time
$i$ : imaginary unit

For digital signals, the Discrete Fourier Transform (DFT) is used:

X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i \frac{2\pi}{N} kn}

where:

$X_k$ : k-th DFT output
$x_n$ : n-th input sample
$N$ : number of samples
$k$ : frequency index
$n$ : input index

The Power Spectral Density (PSD) can be estimated using the Welch method, which divides the signal into segments, applies a window function, computes the DFT, and averages the results. In MATLAB, this is done using the pwelch function.

\text{PSD} = \frac{1}{N} \left| X_k \right|^2

Uncertainty analysis

In uncertainty analysis, the total uncertainty $\delta R$ in a result $R$ is calculated using the root sum square (RSS) method:

\delta R = \sqrt{\left( \frac{\partial R}{\partial a} \cdot \delta a \right)^2 + \left( \frac{\partial R}{\partial b} \cdot \delta b \right)^2 + \cdots}

For repeated measurements, the uncertainty of the mean is:

\delta \bar{y} = \frac{2\sigma}{\sqrt{N}}

where:

$\sigma$ : standard deviation
$N$ : number of measurements

The standard deviation is:

\sigma = \sqrt{\frac{\sum_{i=1}^{N} (x_i - \bar{x})^2}{N-1}}

Personal Growth and Research Impact

This experiment helped me grow as a researcher in several ways:

Data Analysis Skills: I became more confident in handling large datasets, especially with spectral analysis and uncertainty estimation.
Experimental Design: I gained hands-on experience setting up wind tunnel tests, from calibration to data collection.
Technical Communication: I practiced explaining aerodynamic concepts through clear documentation and visuals.
Research Approach: I learned how to connect theoretical models with experimental results in a systematic way.

The most challenging parts—uncertainty analysis and spectral decomposition—forced me to think carefully about both the limits and reliability of experimental data, lessons that will carry into more advanced aerodynamic research.

Conclusion

Working on the BeVERLI Hill project gave me a stronger appreciation for how careful measurement and statistical validation are essential in experimental aerodynamics. It also showed me how experimental and computational approaches (RANS/LES) complement one another in modern aerospace research.

This project also sparked new interests for me, including:

Advanced measurement methods for unsteady aerodynamics in rapid maneuvers (e.g., drones)
Applying machine learning to experimental data analysis
Flow separation prediction and control for agile flight systems

Overall, this was a meaningful step in building my research foundation, and it confirmed my motivation to keep pursuing challenging questions in aerodynamics and CFD.

References

Virginia Tech Stability Wind Tunnel Article

AOE Stability Wind Tunnel

NASA Turbulence Modeling Resource

The Critical Role of Aerodynamics: Insights from the NASA-BeVERLI Hill Experiment

Introduction

Summary of Experiment

Key concepts for the experiment

Pressure coefficient

Boundary Layer

Reynolds Number

Mach Number

Spectral analysis

Uncertainty analysis

Personal Growth and Research Impact

Conclusion

References

More Posts

Revisiting the Airworthiness Issues of the L-1011 TriStar Tanker: A Reflection on Engineering Growth

How the Space Environment Impacts Spacecraft Computers